This may come as a surprise, but computers are terrible at math. They blindly execute code and care little for semantics. Computers don’t actually know what the integer “5” or the real number “π” are - they can only encode these symbols as a finite bitstring and run code that emulates the underlying math. This mostly works fine, but rough edges like integer overflow or floating point precision keep things interesting for software developers.

Many of these emulations are only crude approximations of the underlying mathematics and are often unsuitable for tasks like data encoding where we can’t introduce any error because we are expected to decode exactly the original data. Finite fields (also called Galois Fields) allow computers to exactly perform addition, subtraction, multiplication and division over some finite set of elements. Unlike floating point numbers or signed integers, these finite field elements can be used to encode arbitrary bytes; allowing you to solve equations and analyze with exact precision. Pretty much every symbol you’re seeing on this page was encoded into a finite field at some point. Probably many times.

Algebra Refresh

When we learn algebra in school, we’re often just replacing some number with an x or y and manipulating simple equations - but numbers aren’t the only thing that can be algebraically manipulated. In many ways finite fields are very similar to the numbers we are familiar with. But most of the time they are unintuitive and it can be confusing to keep things straight. It’s going to be important to think of these finite field elements less like numbers (representing quantities we can add and subtract using simple arithmetic) and more like abstract symbols that we can manipulate algebraically as long as they obey some simple rules.

A Quick Note on Notation and Terminology
I’m a software engineer. I’m not a mathematician, and my goals here aren’t to explain these concepts rigorously. I will be abusing both notation and terminology. Sorry not sorry.

Groups

A group is a set of elements under some binary operator (denoted ⋅ here) which has the following properties:

• Closed - the result of any operation is an element in the group
• Associative - (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c)
• Identity - there is some identity element (denoted ⍬ here) where a ⋅ ⍬ = a
• Inverse - there is some b such that a ⋅ b = ⍬

So integers set of all integers ℤ with addition form a group - 0 is the additive identity and you can always negate to find the additive inverse for an element. Integers under multiplication are NOT a group, because there isn’t always a multiplicative identity that’s also an integer. We’ll look at this more closely in a bit.

But a group’s elements don’t have to be numbers. Consider this image, which can be “flipped” horizontally or vertically:

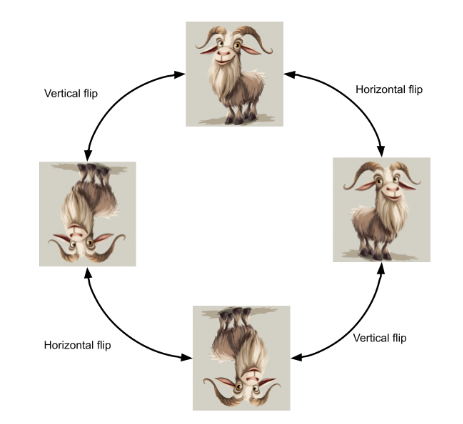
This set of the 4 possible flip functions with function composition form a group. We have the identity element I (do nothing to the image), H (flip horizontally), V (flip vertically) and HV (flip horizontally then vertically) which form our group {I, H, V, HV}. Each element is its own inverse, since we can repeat any flip to “undo” it. Any finite composition of these operations is equivalent to one of these 4, so the group is closed. This group is especially abstract because not only are the elements not numbers, they aren’t even values (they are functions).

It’s tempting to encode these elements in a computer as 2-bit integers {0, 1, 2, 3} - but this group (we’ll call it ℤ(4) to mean the integers modulo 4) has a different structure and so we wouldn’t be able to map integer arithmetic to our group operations (which has to do with this particular 4-element group not being “cyclic”). Instead we can represent each element in the group as a symbol and enumerate all the group operations in a simple table:

	I	H	V	HV
I	I	H	V	HV
H	H	I	HV	V
V	V	HV	I	H
HV	HV	V	H	I

This mostly makes sense:

• If we H then V, we get an HV
• If we HV then V, we get an H (because we “undid” the vertical flip).

This is a contrived example, but there are many examples of groups out there. The point of this simple example is to demonstrate how we can apply these algebraic rules in a way that’s different from the normal arithmetic that we normally deal with as long as we obey the group properties.

Rings and Fields
Groups are simple and easy to construct, but we won’t usually be analyzing complex systems with them. The problem is that groups are too abstract to be very interesting. We need to add more properties (more “structure”) to a group to create more complex algebras.

The integers ℤ have both addition and multiplication defined and so they form a ring. Without going into too much detail, the key part is that the ring under “addition” forms an abelian group (meaning the rules above plus a + b == b + a), and we now have the distributive property (a(b + c) == ab + ac). Rings are much more powerful than groups. But rings also won’t deliver us linear algebra.

What we really need is a field - or a set of elements that have addition, subtraction, multiplication and division. The proper definition is a bit more rigorous, but think of the rational numbers ℚ as an example of a field (the multiplicative inverse of any integer z would be 1/z). Fields add enough structure that we can use them as vector or matrix elements in linear algebra and solve equations.

Finite Fields

Computers have no problem using N-bit symbols to represent a ring - even with underflow or overflow, the various “ring” properties (associativity, additive inverses, etc) hold up just fine. This is because the set of all N-bit integers represents a finite ring ℤ(2N) which has 2N elements. We can have either unsigned or signed (2’s complement) integers but we won’t bother looking at this distinction here. The 8-bit integers for example are ℤ(256) which is equivalent to ℤ modulo 256. This is called “modulo arithmetic”, and is very popular in discrete mathematics commonly used in computers.

But what if we want division too? Here we can try to create a “multiplication table” for ℤ(4) which has 16 possibilities by computing a * b % 4:

	0	1	2	3
0	0	0	0	0
1	0	1	2	3
2	0	2	0	2
3	0	3	2	1

Unfortunately, not all our elements in ℤ(4) have well-defined multiplicative inverses. In the above table, we can see that 2 lacks a multiplicative inverse (the 2 “column” has no elements that multiply with it to give the multiplicative identity 1) - probably because 2 evenly divides our ℤ(4) ring. Without multiplicative inverses, we can’t have division and without division we can’t have a field and without a field we won’t be solving for x. Floating point math is great when we can accept some imprecision, but not when we need exact answers. What if there was some way to ensure that every element in our field had a single multiplicative inverse?

The trick is to make sure our ring has a prime number of elements. If none of the elements can evenly divide the ring, we’re guaranteed to have multiplicative inverses for everything. Now, let’s see what happens when we work with ℤ(5):

	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
2	0	2	4	1	3
3	0	3	1	4	2
4	0	4	3	2	1

Now we can see that each non-zero column has a 1 in it (the row tells us the multiplicative inverse).

While ℤ(p) works as a finite field, it’s not the most efficient solution for computers. Remember - computers want to process in bits and bytes. ℤ(5) would need to be represented in 3 bits but this means we are only using 5 of our 8 possible symbols. It’s also challenging to split up our data on boundaries that are not byte-aligned, which can result in a lot of extra computation overhead.

Polynomials

So the modulo ring ℤ(p) works fine as a finite field, but it’s not efficient because computers want to use base-2 bits and bytes. Fortunately for us, 2 is actually a prime number and so ℤ(2) is a field! Unfortunately, it’s too small to do much with, and we can’t really arbitrarily string these 1-bit elements together to get larger field elements (just like we can’t multiply or divide large numbers digit-by-digit). But we can use these 1-bit fields to construct arbitrary finite fields using polynomials.

If you remember, a polynomial is just an expression like x^3 + 2x^2 + 1x + 3. Although not exactly the same, our decimal numbers can be seen as polynomials where we evaluate with x = 10. For example 145 is 1x^2 + 4x + 5 with x = 10. In the same way that we can “extend” our base-10 digits to hundreds, thousands and beyond, polynomials also allow us to extend the underlying field to arbitrary sizes. Conveniently, the long-form addition and multiplication that we learned in school can also be used on polynomials, which means that polynomials also form a ring.

Let’s revisit our example of ℤ(4) which is a 4-element ring but not a field. How could we get a 4-element finite field by extending ℤ(2) with polynomials? We’ll interpret each of our 2 bits as a 1-bit coefficient to a polynomial: Ax + B. We can trivially add or multiply these resulting polynomials, but like with integers we need to introduce a ‘modulo’ (otherwise we may find ourselves needing an x^2 term which exceeds our 2 bits).

With ℤ(5), we’re doing all our operations modulo the prime number 5. This keeps everything nicely bounded and ensures that each element has a multiplicative inverse. When it comes to polynomials, though, we need something similar—a special kind of polynomial called an “irreducible” polynomial of degree 2. Think of it like the prime number of the polynomial world. This gives us a finite field with 4 elements: 𝔽(4).

Irreducible polynomials can’t be factored into a product of two simpler (non-constant) polynomials. Sometimes, you’ve got a bunch of irreducible polynomials to choose from, and which one you pick is mostly up to you—unless you’re doing cryptography, where absolutely nothing is left to chance. For this simple example, we’ll choose x^2 + x + 1 as our irreducible polynomial. Our ℤ(4) has the following elements: {0, 1, x, x + 1} which can be encoded as {00, 01, 10, 11} respectively. Here’s the multiplication table for this field:

	0	1	x	x+1
0	0	0	0	0
1	0	1	x	x+1
x	0	x	x+1	1
x+1	0	x+1	1	x

It’s worth explaining a bit how x^2 = x + 1. If we were to blindly multiply this out, x + x is obviously x^2. But remember we want to keep everything in our set of 4 elements, and x^2 can’t be represented in our field of 4 elements. So we reduce (like a modulo) by our x^2 + x + 1 polynomial to get a remainder of x + 1. This is similar to how we take 3 * 3 = 9 mod 5 = 4 in ℤ(5).. We can do long-form division on the polynomials to do the same: x^2 mod x^2 + x + 1 = x + 1 because if we try to divide we get 0 with a remainder of x^2, then we can subtract leaving us with -x - 1 which, because our coefficients are ℤ(2), is x + 1.

Conclusion

While this example with 𝔽(4) is small enough to be enumerated completely here, the beauty of finite fields is that they can be extended to arbitrary sizes. Whether it’s a 256-element (8-bit) field or a massive 4-billion-element (32-bit) field, we just need to find an irreducible polynomial of the right degree. With 𝔽(256), for example, we can encode each byte as a single element of the field, making the data much easier to work with. AES encryption uses “Rijndael’s Field” which is reduced by x^8 + x^4 + x^3 + x + 1. With 𝔽(256) we can treat data as vectors or matrices over these field elements, allowing computers to encode and process information more efficiently. Modern CPUs include “carryless multiplication” and Galois field instructions to accelerate most of these operations because they are so commonplace.

Finite fields were first discovered by Évariste Galois in 19th century France as he studied solutions to polynomial equations like quadratics and quintics. He scribbled his groundbreaking ideas into several letters the night before he was killed in a duel at the age of 20. Who knows what other insights the world lost that fateful day, but I often wonder about what he might say if he knew how his work has become foundational to modern data storage and communications.